I found this puzzle in a tiny but mighty pocket puzzle book named Optical Illusions.
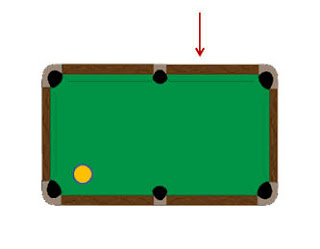
Suppose the yellow billiard ball strikes the bumper at the point identified by the arrow. If the ball has the energy to keep rolling, which pocket will it eventually sink into?
Let's identify pockets as upper or lower, left, center or right.
Your answers are accepted any time until midnight Eastern Time on Sunday, on our Family Puzzle Marathon.
Suppose the yellow billiard ball strikes the bumper at the point identified by the arrow. If the ball has the energy to keep rolling, which pocket will it eventually sink into?
Let's identify pockets as upper or lower, left, center or right.
Your answers are accepted any time until midnight Eastern Time on Sunday, on our Family Puzzle Marathon.













18 comments:
Upper left. I think it will follow the path similar to 3 cushion billiards. Donald Duck did a great job teaching that one!
4 of my students say the bottom center and 5 of my students say the bottom right. We used a protractor and straightedge to get these guesses. The group of 4 says it will hit 2 bumpers to get to the bottom center. The group of 5 says it will hit the bumper right beside the bottom center causing it to hit 2 more bumpers and continue on to the bottom right.
Here is the link to the diagram I used to solve this puzzle. It is likely not the shortest way; I can hardly wait until Monday morning to see what the answer is.
http://s973.photobucket.com/albums/ae218/jcherry_99/?action=view¤t=billiards.jpg
I'm not sure if the link works: It seems to expose all my other diagrams (one).
In case you cannot see the diagram
Techical: The original diagram has been enlarged 200%.
Answer: as you look from above the table the ball goes into the upper left corner.
Description: (Just in Case)
First bounce: upper edge: Angle of incidence = 50o (40o was easier to calculate)
Second bounce: right edge: angle of incidence 40o
Third bounce: lower edge: angle of incidence 50o
Three bounces are enough to put the ball in the upper corner.
It will end in the lower center pocket
Billiard balls usually hit and change directions at 90 degrees. I checked with my hands and then got a carpenter's square out and I think it goes in the upper left hand corner pocket.
Gurubandhu
I've already submitted what I consider to be the easiest answer, but I think this can be done by banking off any wall first and then go either for another wall or the arrow. However, I think the math would be terrible if one does not know the method used that relates the ball's position and the length and width of the table.
Nice shot! Seems like upper left. I printed out the rectangle, and traced the path of the ball. To simplify the task, I did not fuss with the side bounces, but instead used the "mirror effect", extending the original upper and lower "bumper" lines further to the right, and constructing few isosceles triangles with help of a ruler, such that they represented the path of the ball with the angle of incidence being equal to the angle of reflection (thus the isosceles triangles). I then compared the points of ball's touching the "imaginary" bumper lines to the locations of the pockets on these lines and found the one location that was a close enough match. I then transposed the match to its actual location on the table and that was the upper left. Of course my measurements were not absolutely precise, but it seems like the pockets in general allow for certain deviation from the precise hit and I did not have to measure too many times to introduce a huge error.
I am not a pool or billiards player, but I believe that, assuming that the yellow billiard ball was shot within any side spin, then the ball will bounce off the top bumper at the same angle it approached it, and it will:
* next hit the right bumper at about 40% of distance between the side pockets, measured from the right bottom pocket, and
* then will hit the bottom bumper between the center and right pockets, and
* then will travel into the upper left pocket of the table.
If the billiard ball was hit with side spin, then I think it will deflect off the top bumper at a different angle than it approached and that it could end up in another of the table pockets including possibly the upper right pocket or lower right pockets.
It will be.... the upper left corner.
Billiard ball is reflected off the walls of the table similarly to the light ray. It means that it goes out at the same angle it came in but in the opposite direction. See the graphical solution below. Afterwards, click the "Back" button of your browsers to come back to this page.
Solution demonstration.
I found the Donald Duck video some of you refer to. It doesn't really talk about angle math but it describes how to win in billiard using the diamonds that are usually inscribed around the pool table. Donald Duck video.
A puzzle point for those who correctly pointed the angle: Jerome, Gurubandhu, Ilya, TracyZ.
I felt I had to abandon the puzzle last week only because I know that on a pool table (or billiards) the reflection is imperfect, there is always some "slippage" and the angles don't actually behave like light rays. And there is spin, and it really does matter. The northwest corner is the best guess, yes.
I *strongly* disagree with your solution to this puzzle. The ball will bounce off the cushions of the billiards table, but these points are not as you have shown in your picture. They are closer in. You have shown the ball bouncing off the sides of the table at the points where the cushion is connected to the table, not where the ball meets the cushion. See here, http://HawaiiMathTutor.com/temp/billiards.com for a pic that shows the true nature of the ball's travel. I don't think we can accurately predict where the ball will end up.
Thad - I am not sure I understand your point. I agree that this puzzle assumes an ideal environment: perfect reflection and ball keeping its energy all the way that is just an approximation of a real environment. I also agree that my drawing is rough and lines go all the way to the table boundary instead of bouncing off the cushion but I think the general direction will be the same...
Your pic link below doesn't work, can you check it please. I would love to see your explanation.
It's really strange photo, i'm trying to find out your question, but can't, can you write to us your question answer
I drew this one more time by relaxing the rule of assuming that the cue ball must go first to the point that is on the upper right first.
My first bounce went to the right bank and then to the upper right arrow. The result was the same: the cue ball goes into the upper left corner. I haven't tried boucing it off any other bank nor letting bounce twice before hitting the arrow.
I think we should just assume that it must go to the arrow first.
Sorry, the correct link to my pic is http://HawaiiMathTutor.com/temp/billiards.jpg.
I grew up in a bar owned by my parents. It's upper left.
No one considers spin and english..
Thad - I checked your drawing and now understand what you meant. You are right - my drawing is not accurate. I didn't notice the green bumper. The original drawing should be modified to shift the red arrow so that the ball will eventually lead to the upper right pocket.
Post a Comment
Note: Only a member of this blog may post a comment.